Many years ago, one of my students wanted to skip Algebra 2/Trigonometry. The teachers at his school gave him all of the tests and study guides from the year, except for the final. If he could score 90%+ on the final, they’d let him skip the course. He was an exceptional student – he breezed through the material, scoring a 97% on the final – but one topic always bothered him. He could never quite get comfortable with the Statistics and Probability unit.
He’s not alone. There’s something about this topic that just isn’t intuitive. Here’s an example:
You’re flipping a coin 8 times. Which sequence is more likely?
TTTTTTTT
THTHTHTH
Here’s another one:
A six-sided die has four green sides and two red sides. Which sequence is most likely?
A) RGRRR
B) GRGRRR
C) GRRRRR
And here’s one more:
Which yogurt sounds healthier?
A) 90% fat free
B) 10% fat
In each case, the right answers1 somehow don’t feel right, at least not initially. It’s easy enough to learn the right approach to each question. It’s harder to recognize these concepts in real life, and to respond with the ‘right answer’, especially when that response will require considerable effort over several months.
There’s a concept like this in test prep. Applying it correctly doesn’t feel right initially, but it leads to much higher scores. That concept is expected value.
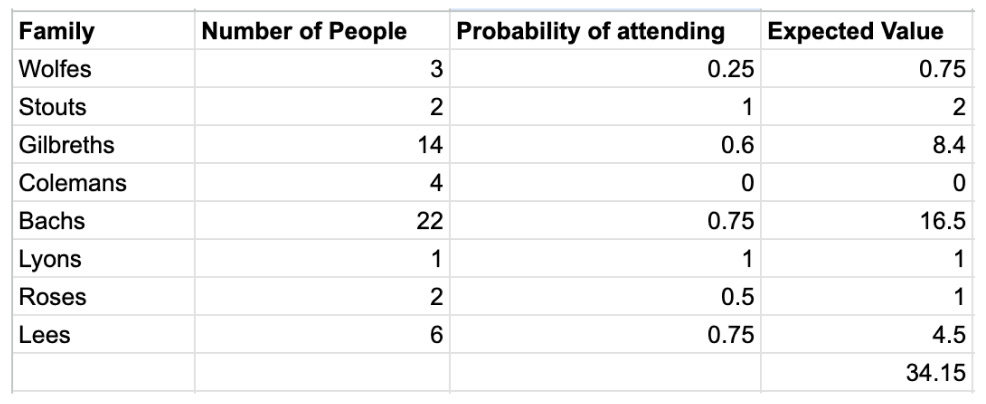
My wife and I used expected value when we were planning our wedding. We were inviting a lot of people. We needed to know how many people were actually going to come, but we weren’t getting RSVPs quickly enough. We couldn’t just assume that the non-responders weren’t going to come…but it didn’t make sense to assume that they were all going to come either. So we used a table like this one:
I multiplied the number of people in a family by the probability that they’d attend. The result was the ‘expected value’ of their attendance. The individual expected values were absurd – you can’t have 16.5 Bachs attend your party. But when we added up all of the expected values, the sum predicted the eventual attendance quite accurately.
Sports gamblers use a similar technique2. Let’s suppose the Raiders are not expected to win the Super Bowl (shocker). Vegas will pay you $50,000 if they do, and you only have to put down $100. This implies a 0.2% chance that the Raiders will win. But let’s also suppose that you think those odds are too low. Yes, they are terrible and quite unlikely to win…but according to your sophisticated model, they actually have a 1% chance of winning.
Expected value of winning: $50,000 x .01 = $500
Expected value of losing: $100 x .99 = $99
Expected value of this bet: $500 - $99 = $401
Now, even if you have an excellent prediction model, it would be very foolish to place all of your money on this bet. You only have a 1% chance of winning! But what if you had 100 different bets, each with a positive expected value? If your model is correct, then you can simply find the expected value of each bet, add them all up, and predict your winnings for the weekend.
This same approach is very helpful when preparing for standardized math tests. The ACT provides a particularly good example. So many different problem types appear on the ACT – you can’t afford to “bet” all of your time on just one. Instead, you need to perform a sort of expected value calculation for each type: What is the likelihood that working on this question will lead to points?
Your calculation must take into account what you already know, what you don’t, how likely the concept is to appear, and how easy it is to learn. If something has no chance of showing up, or you already know it, or you have no chance of learning it, then it’s not worth your time. On the other hand, if something has a high chance of showing up, and you haven’t learned it, but you could learn it quickly, then that’s a problem worth working on.
For most students, these calculations yield a high number of questions, most of which have a relatively low expected value. As a result, you unfortunately need to adopt a sort of ‘gatherer’ approach. And I say ‘unfortunately’ because what we all prefer is a ‘hunter’ approach, like the one we use when preparing for school tests: For days at a time you stalk one prey – maybe solving quadratic equations, or graphing ellipses. If you learn everything about your target and execute on test day, you’ll get a good score. This is not an easy process, but it is a very simple and satisfying one.
ACT math tests aren’t like this at all. A Law of Cosines variation shows up on E23. It’s not there on E25, but it reappears on Z08, this time in a slightly different form. It would be foolish to hunt the Law of Cosine questions like you would in school – only a small number of very specific variations appear on the test.
But you can’t ignore them either. They show up ~50% of the time. To score 30 or higher you’ll most likely need to get at least 50 questions right, so you can’t afford to ignore any question that has even a 10% chance of appearing. And, of course, I’m just using the Law of Cosines as an example. There are also logarithms, fractional exponents, matrices, and many more.
Luckily, these questions are rarely difficult. Almost every question on the test, with the exception of the 2 or 3 hardest ones, would be pretty easy if you were studying that unit in school. If you could just gather all of these variations and keep them fresh in your mind at the same time, you’d get a very high score. But there are a lot of them. And it’s hard to know which ones will show up.
So what do you do? Adopt the gatherer mindset. Systematically target all of the high-value question variations: maybe perpendicular lines, then special right triangles, then Law of Cosines…Yes, there are a lot of question types, but it’s not an insane number. When you start, your field3 of high-value questions might look like this:
If you keep practicing high-value questions, the field will look more like this:
In the moment, this approach doesn’t feel right to most students – you practice one random variation, then move on to something completely different, followed by yet another totally different variation, with no end in sight. It feels better to practice 10 ellipses in a row, or 10 matrix multiplication questions in a row. But this ‘hunter’ approach is like betting all of your money on the Raiders.
If you can instead pursue the questions with the highest expected value at all times, you’ll eventually gather all of the high-yield questions and maximize your scores.
In the case of the coin, the two sequences are equally likely: .5 raised to the 8th power. In the case of the die, many people select “B” because there are more Gs. But sequence A is actually more likely – it has the same letters as those in choice B, without having to roll that extra G in front. And as for the yogurts…we all know they are the same, but somehow the “90% fat free” option just sounds healthier!
These three sites were helpful: https://www.foxsports.com/articles/nfl/raiders-futures-odds-to-make-nfl-playoffs-super-bowl-odds | https://www.techopedia.com/gambling-guides/what-does-ev-mean-in-betting | https://sportshandle.com/expected-value/
This image is adapted from a Mathchops onboarding guide we made in partnership with Test Bright. Let me know if you want the full guide. (It’s free.)