Difficulty vs Category
Which is more important for question selection?
You’ve been working with an SAT student for one month. She is going to work on 50 math questions this week. You can either choose the difficulty (750 - 800, 700 - 750, 650 - 700, etc) or the category (10 of your choice – things like linear equations, geometry). But you can’t choose a combination – it must be one or the other. Which would you choose?
After a practice test, many parents will ask, “What are the concepts she needs to work on?” Tutors commonly respond to practice tests by assigning concept-focused worksheets. In both cases, the assumption is that certain concepts are responsible for lowering the scores.
In a school setting, this assumption is correct. If a student has trouble factoring quadratics with leading coefficients, and she’s about to take a test on factoring quadratics…she better learn to deal with leading coefficients. One concept could easily lower your grade by 10-20%.
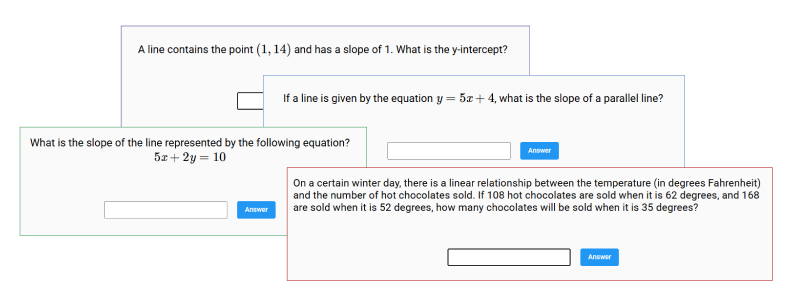
But nearly everything a student learns in Algebra and Geometry is fair game on the SAT. There are lots of concepts. And within those concepts, there are lots of variations. You may have trouble with linear equations…but which ones?
Missing a question about the slope of a parallel line is one thing; missing the hot chocolate question (see above) is quite another.
And that’s why I believe that difficulty is more important than category. I only want the student working on that hot chocolate question if it’s at or below her level. Missing it doesn’t necessarily indicate that she needs to practice lots of other linear equations, because the hot chocolate question is very hard. Maybe she’s very good at most linear equations! It’s the relative difficulty that matters – whether it’s easy for the student – not the category.
In fact, if I had to come up with my definition of a valuable question, I wouldn’t even mention categories: A good question 1) shows up a lot on real tests 2) would currently defeat my student 3) is below the level of my student.
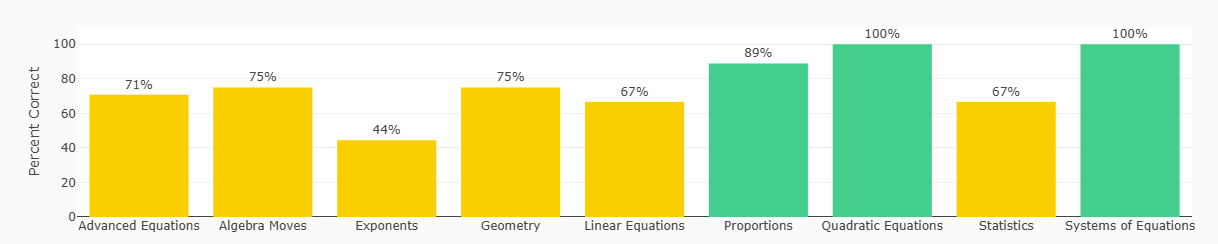
Finding these questions is not easy. And the category is sometimes an important clue. If I see a performance chart like this on Mathchops, I know we need to focus on Exponents:
It is also sometimes helpful to focus on one category at a time, so that it’s easier for the student to remember what she learns. We do that through category challenges:
But even here, the categories are still organized by level. A student with a low percentage on Exponents probably does not need to work on all of the Exponents questions – just the ones near her level.
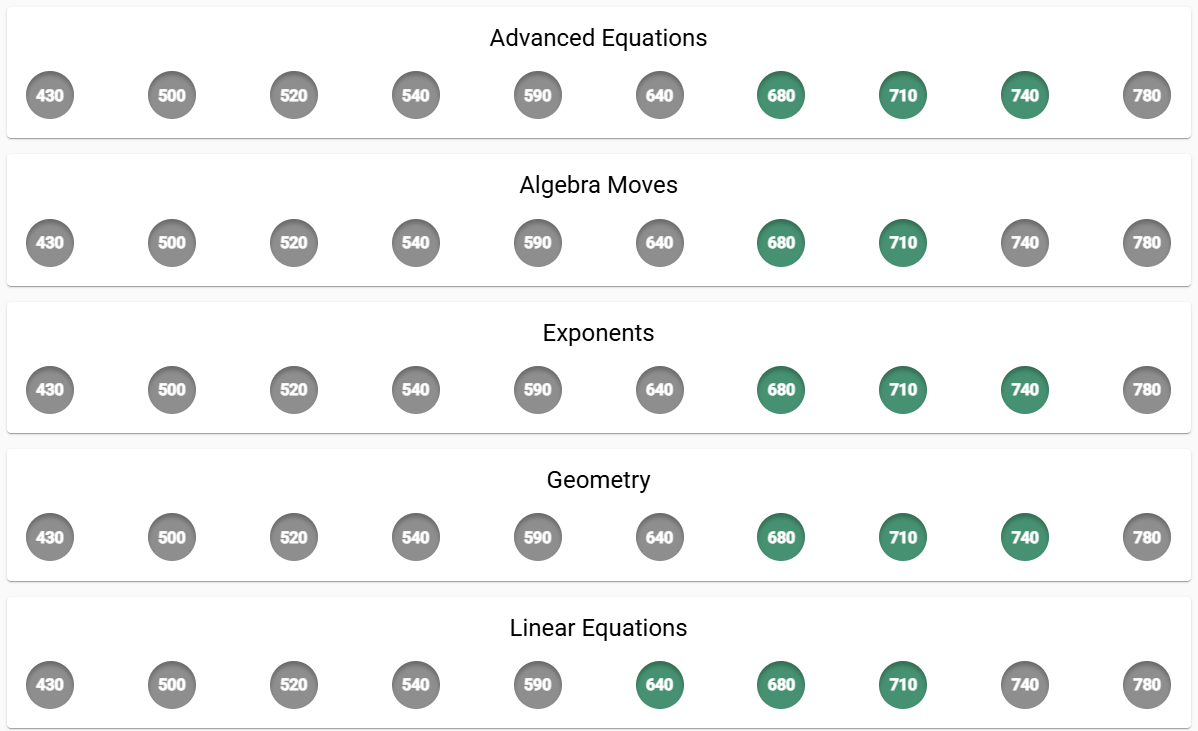
And it’s actually pretty rare for a student to do much worse in one category. This is what most of my students’ category performance charts look like:
Some are higher than others, but they all tend to fall in that 60-80% range.
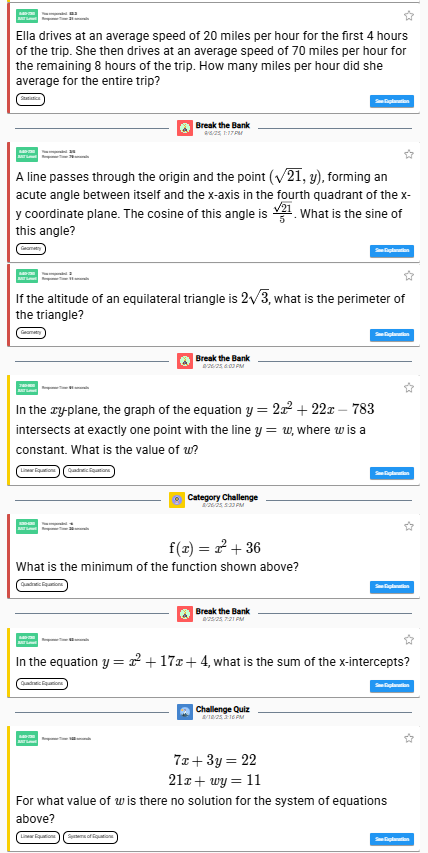
So we are back to that same problem: how do we find common questions that defeat our students now but will be easy for them to master? I do it through Mathchops – the point of the games is to find these questions and deliver them in an engaging way. Then I can review them on a student’s Analyze page:
I’ve filtered by “missed questions” so that you can see that the wrong answers are scattered across different games and categories. If my student chooses to work on Systems or Linear Equations, I have no problem with that. But I mostly want him working on missed questions at or below his level.




I agree. Topical categories are for math teachers, pragmatic categories are for testing students and their trainers.
One version of my still evolving spiel: There are three kinds of math questions: 1) ones you can do, no problem; 2) Ones you can do but are hard; 3) ones you can't do
Then I point out that there are really no questions in category 3, we will work to move all the Cat 3 questions into Cat 1 or 2, and most of the category 2 questions int Cat 1.
Then, later, I'll point out that there are two category 1 questions: 1a) the ones you do just fine, and 1b) the ones you could do faster, thus giving extra time to work on the few remaining cat 2 questions.