Motivating Students With Visions
How to get students to do the work they've been avoiding for years
Every student reaches a point when math scores stop going up. Maybe they were increasing easily for a while, as the student became more familiar with the test, but now all the easy points are gone. The scores can still go up a lot, but only if students master the skills behind the questions that are blocking them.
This is work that most students are not excited to do. They’ve been avoiding these skills for years – things like percents, fractions, algebraic operations, completing the square. Now they need to actively seek these skills out and master them. Part of the tutor’s job is to motivate the student to take on this unpleasant work.
As I mentioned in another post, students are primarily motivated by scores. But the work you want them to do is often not directly tied to a score. It’s tasks like figuring out why you got questions wrong, redoing them multiple times, and finding similar questions to practice. These tasks don’t yield score predictions, as an official practice test would.
What will motivate them? I think you need to share your vision. Why am I giving you all this work? How, exactly, will this work lead to higher scores? Without this vision, they are unlikely to take on the pain and frustration that significant improvement requires. They’ll rage-quit the Level Challenge on Mathchops and never try again.
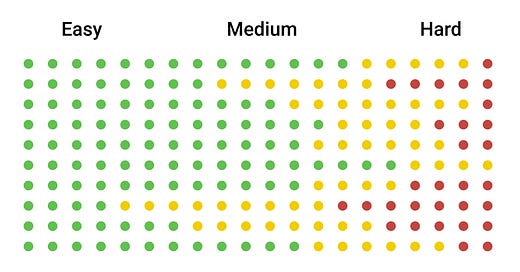
This is the vision I share with students: “Imagine there are 1000 possible questions on the test. They are arranged in a grid, represented by dots. As you go from left to right, the questions get harder. Each row represents a category, like systems of equations or quadratics. This is what your grid looks like now:
We aren’t going to spend any time on those green questions – you’re already getting them right, and if they show up the test, you’ll probably get them right there, too. And we won’t spend too much time on the red ones either – those are the super hard ones that take a long time to explain and a lot of work to remember. But those yellow ones are very valuable. They are the ones you used to know and could remember pretty easily, or the ones I could teach you in about 30 seconds. We want to find those and do everything we can to keep them fresh.
But how are you going to find those questions? I know what’s on the test, but I don’t know what you know. You kind of know what you know, but you don’t know what’s on the test. That’s where Mathchops and redos come in. They are systems for finding great questions and helping you master them efficiently.”
When I explain this vision to students, they are much more open to difficult work. It may still be unpleasant, but now it’s directly tied to a goal they deeply care about.